Student Research Showcase
In the Spring, the Mathematics Department hosted the 2017 Showcase of Student Research in Mathematics. The Showcase featured five participating undergraduate and graduate students and each student gave a 20-30 minute presentation on their research projects.
Speaker: Kelly Christensen
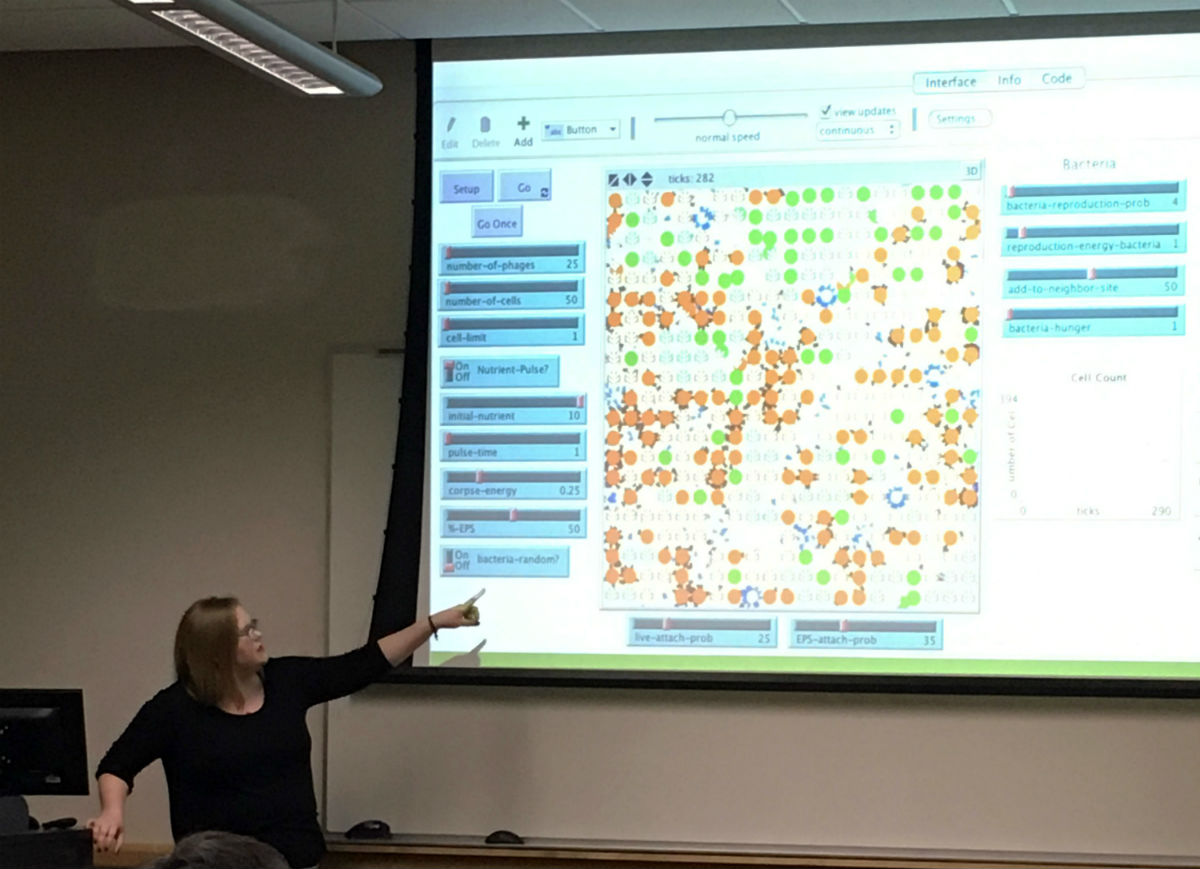
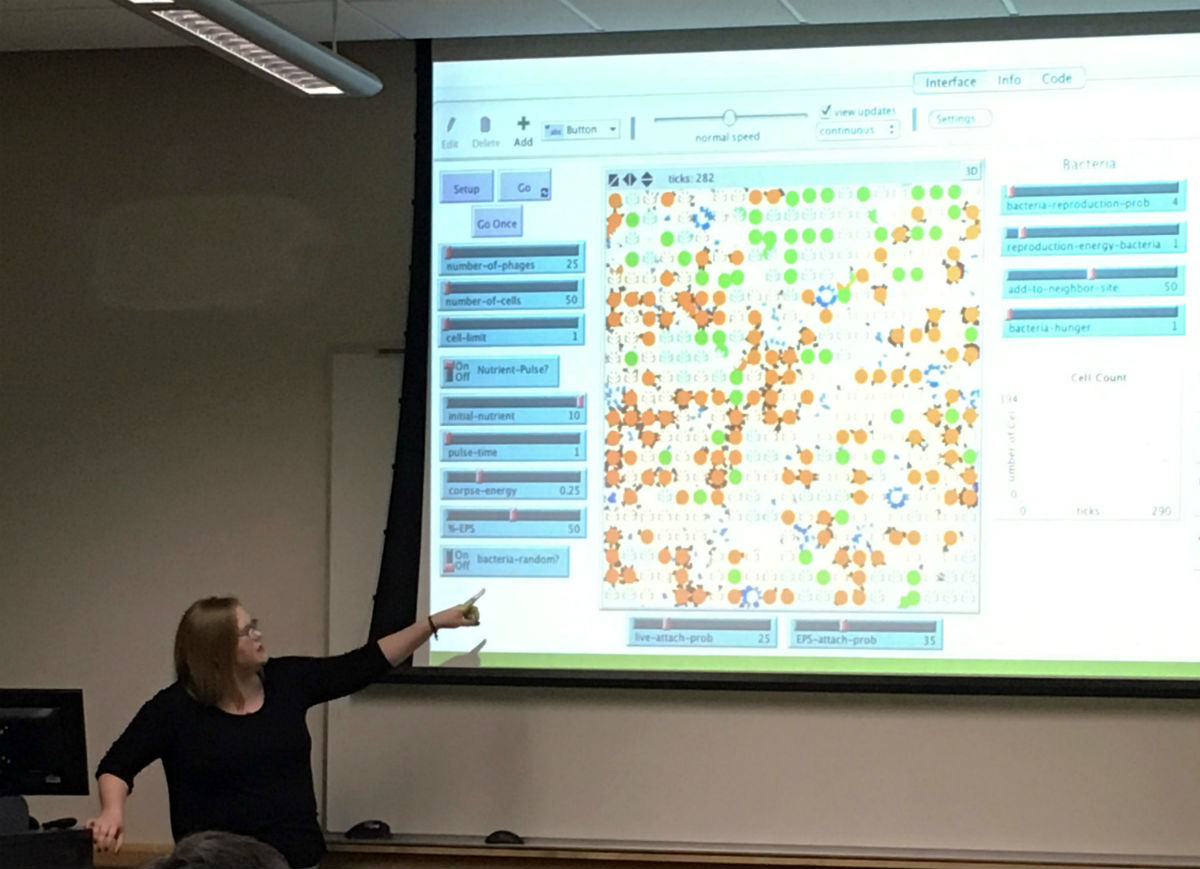
Title: The Impact of Spatial Structure on Phage-Bacteria Interactions
Abstract: Phage (viruses that infect bacteria) produce a burst of progeny upon lysis of a bacterial cell. “Phage therapy” (as an alternative to antibiotics) has thus far not lived up to initial expectations. Lab experiments have shown that bacteria are able to survive even when phage density is high. Additionally, surviving cell densities in biofilms are orders of magnitude larger than in liquid cultures. We constructed two models (an agent based model and an ODE model) to examine various bacterial protection mechanisms and how these are influenced by spatial structure. In some cases, coexistence of phage and bacteria was a consequence of self-organization that segregated phage and bacteria, with most bacteria surviving in regions with phage sinks and most phage lurking in complementary areas.
Speaker: Dorothy Catey
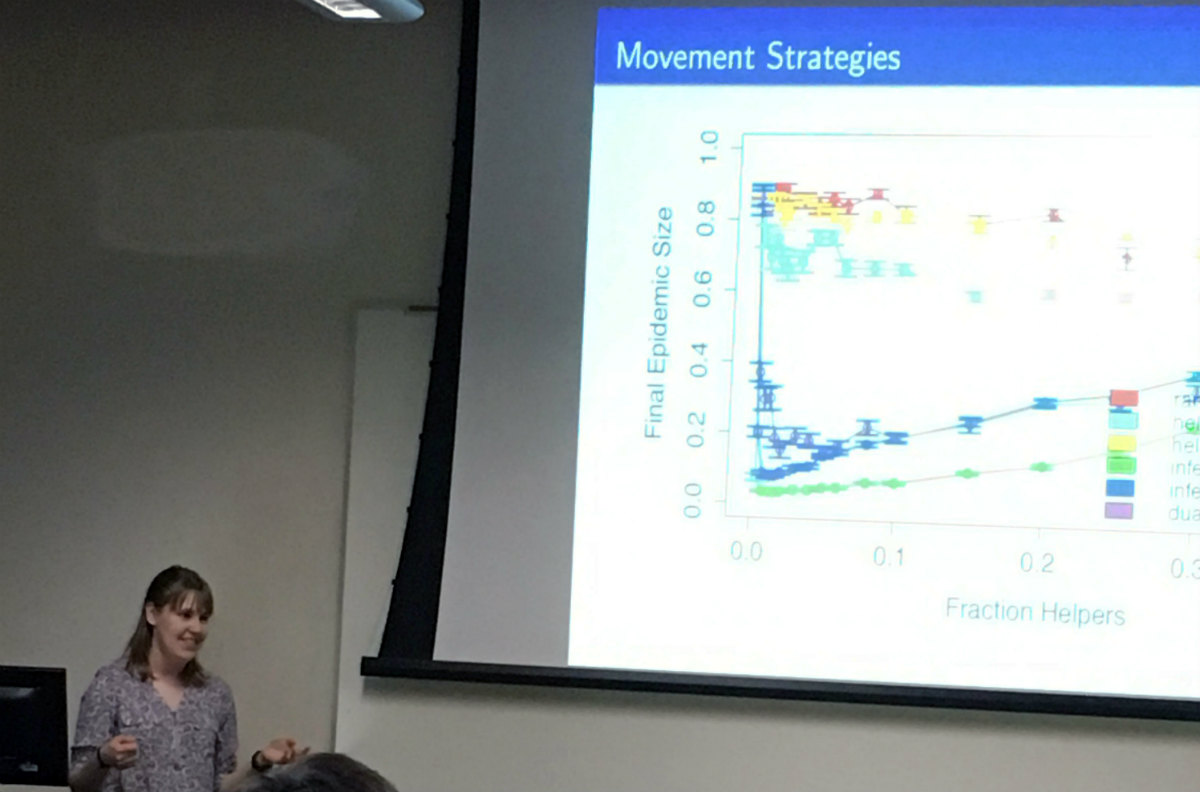
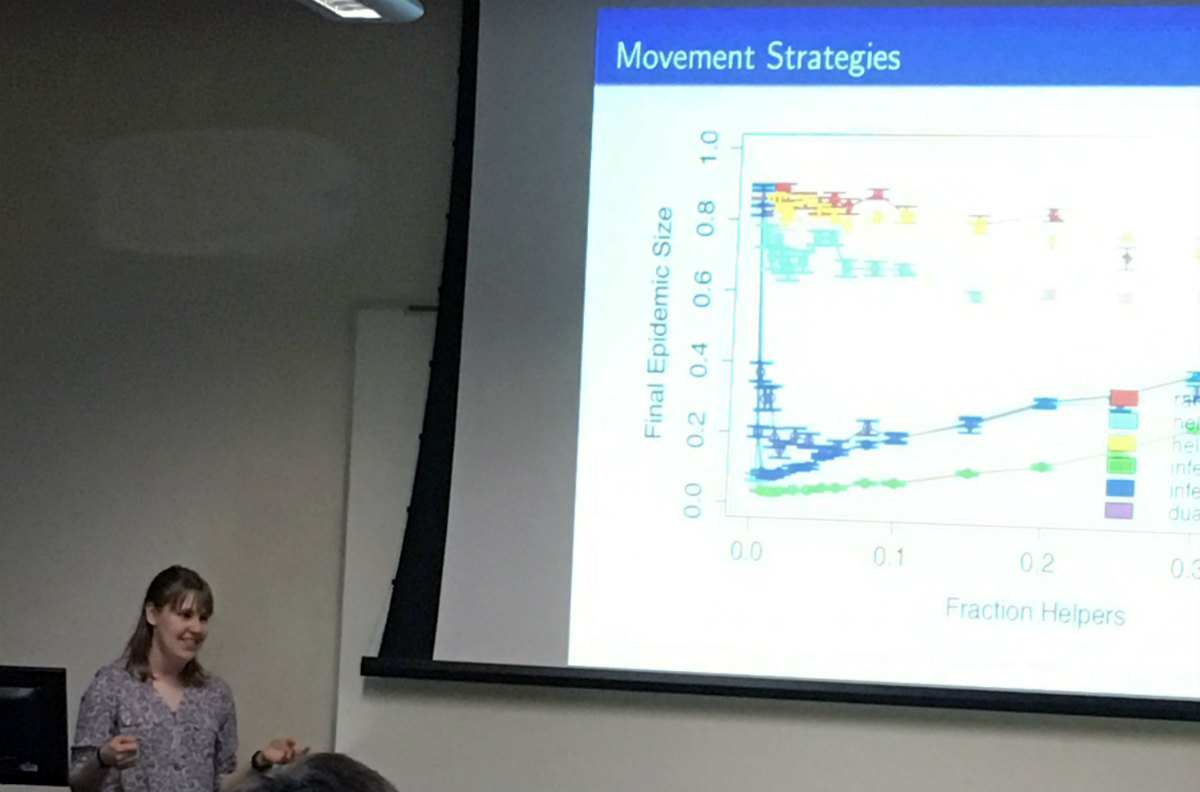
Title: Seek vs. Sought: Movement Strategies in Epidemics
Abstract: When a disaster, such as an epidemic, occurs, a common response is to flood the affected area with volunteers. Organizations like the CDC and WHO implement intervention strategies such as contact tracing, quarantine/isolation, vaccination, and treatment, which have often been studied using epidemiological models at the institutional or access level. We are interested in studying implementation at the individual level. We construct a simple agent-based model that has an SIR-like structure in order to study the effects of movement strategies and to inform decision-maker intuition. We find that the movement strategy chosen by volunteers can have a large impact on the attack rate of the disease.
Speaker: Daniel Reiss
Title: Fourier Coefficients of Siegel Paramodular Forms and Paramodular Hecke Operators
Abstract: Modular forms are periodic functions, and as such have Fourier expansions. The Fourier coefficients of elliptic modular forms satisfy certain arithmetic properties and are related to the eigenvalues of Hecke operators. Much work has been done of late to produce similar results in the theory of Siegel modular forms, which are a natural extension of elliptic modular forms. In current research we seek to fill some of the gap for Siegel paramodular forms. In this talk we will present the known results and discuss where we are trying to fill the gap.

Speaker: Jordan Hardy
Title: Fourier-Jacobi Coefficients of Twists of Siegel Modular Forms
Abstract: Modular Forms are defined to be functions of a complex variable satisfying a certain restrictive set of functional equations. For such a restrictive set of objects, they appear in a variety of contexts; originally appearing in the work of mathematicians such as Jacobi, Dedekind and Klein, they have far-reaching applications in analysis, algebra, topology and number theory.
Two generalizations of the modular form are the Jacobi form and the Siegel modular form. A degree two Siegel modular form has a Fourier-Jacobi expansion written in terms of Jacobi forms. The goal of my research is to write the formula for a twisting function developed by Johnson-Leung and Roberts in a (hopefully) cleaner way using the Jacobi-Fourier expansion.

Speaker: Brenna Peever
Title: Crossing Fans of Segments Determined by a Finite Point Set
Abstract: Let S be a finite set of points in the plane in general position. We investigate the number of points S must contain in order to guarantee the existence of specified patterns of intersecting segments determined by S. Specifically we are interested in “fans” of segments sharing a single point of S in which each segment in the fan is crossed by a single segment or set of segments.